Ela surge em áreas como a acústica, eletromagnetismo, e dinâmica dos fluidos. A partir disso, podemos reconstruir a aparência da corda a qualquer momento e repetir isso para momentos diferentes. Equação Fundamental da.
Encontrar a função u (x, t) é o que queremos dizer encontrando uma solução para a função de onda. Para calcular o comprimento de onda refratada, utilizamos a Lei de Snell, utilizando a relação com comprimentos de onda : O comprimento da onda refratada será 7mm. Soluções da equação de onda (uma outra forma de se checar) Beleza, então, se uma dada função representa uma onda , ela tem que satisfazer a equação diferencial de onda.
Mas isso também equivale a dizer que a função é uma solução da equação diferencial de onda. EXERCÍCIOS SOBRE A EQUAÇÃO DA ONDA 1. Uma antena de transmissão de telefonia celular situa-se no topo de uma torre de 15m de altura. A frequência de transmissão é igual a 9MHz, e a intensidade da radiação emitida varia com a distância em relação à antena, conforme o gráfico a seguir. E finalmente a equação da onda de Schrodinger.

Onde i representa uma unidade imaginaria que é usada em planos cartesianos, Ψ quer dizer a função da onda e h significa o operador de Hamilton que seria a energia total de um sistema. A equação de onda Utilizando as quatro equações de Maxwell e um pouco de álgebra vetorial,. As soluções para a equação de Schrödinger descrevem não só sistemas moleculares , atômicas e subatômicas , mas também os sistemas macroscópicos , possivelmente, até mesmo todo o universo.
No entanto, já que não há influências externas na velocidade da onda , você usará a constante para a velocidade da luz, cujas ondas eletromagnéticas viajariam baixo nessas condições. Configuração de uma onda periódica propagando-se num meio com velocidade v Ao estudarmos as ondas vimos que elas têm origem em meios elásticos, como em cordas, na superfície da água, do ar etc. Sendo assim, ondas são movimentos oscilatórios que se propagam num meio. Agora iremos substituir a equação da onda com derivadas parciais por uma equação de diferenças finitas. A equação da onda é um exemplo de equação de derivadas parciais do tipo hiperbólico.
Física Quântica que descreve a evolução de uma onda de probabilidade através do tempo e nos diz que não há como saber onde exatamente uma partícula está em dado momento, mas apenas a região do espaço onde há probabilidade de encontrá-la. UFRS) uma onda esférica, gerada por uma fonte puntiforme, propaga-se num meio não-absorvedor. A energia que incide por segundo sobre uma superfície de 1m colocada perpendicularmente à direção de propagação da onda , a 1km da fonte, é joules. As energias que incidem por segundo sobre a mesma superfície, colocada nas mesmas.
Ondas em um domínio infinito devido a perturbações iniciais bre enas das impedâncias. Deste fracas pelo fator T. A onda total na lateral de incidência é, no entanto, muito diferente. Você pode alterar a fórmula da equação com álgebra para descobrir o valor do comprimento de onda.

Se você sabe a energia do fóton, é possível calcular o comprimento de onda. Note-se que usamos, por simplicidade, a letra y em lugar da letra grega η. Considere uma onda se propagando a uma velocidade v, por exemplo, numa corda levemente tracionada. Seja ainda um sistema cartesiano ortogonal. As expressões matemáticas das funções de onda possibilitam determinar a probabilidade de encontrar o elétron na vizinhança de um ponto próximo do núcleo.
Para expor o método de obtenção da equação da onda , consideramos um problema bidi-mensional: a membrana vibrante. A contribuição reside no fato de a dedução não se basear em um sistema de coordenadas particular. Amplitude: é a altura da onda , é a distância entre o eixo da onda até a crista. Quanto maior for a amplitude, maior será a quantidade de energia transportada.
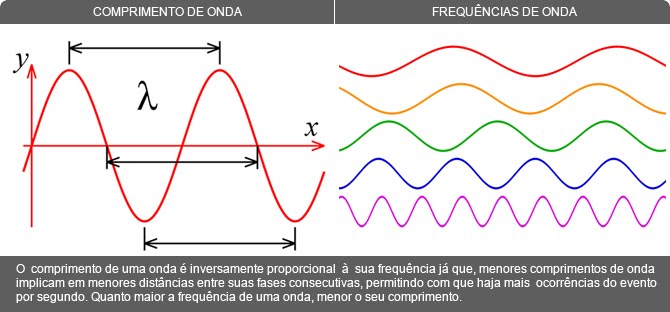
Vamos denotar por upx;tqo deslocamento vertical da ponta no ponto ⁄x ⁄L no instante t ¥0. Porém, a freqüência é uma grandeza inversamente proporcional ao comprimento de onda (λ), isto quer dizer que ondas com alta freqüência têm λ pequenos. Se considerarmos uma corda esticada horizontalmente, u(x,t) nos indica o. No caso particular da equação da onda , este erro se apresenta sobre a forma de dispersão numérica.
Geralmente, este problema se manifesta gerando oscilações não continuas na forma temporal do pulso sísmico. Quaisquer funções ou conduzem a soluções particulares da equação de onda. Para cada valor de , a função é idêntica à função , em , mas deslocada no sentido negativo do eixo dos de uma distância igual a. A amplitude pode também ser lida como a altura da onda. Calcular a amplitude em algumas equações é fácil como fatorar um número, se a equação seguir um padrão. Por essa razão, a velocidade da onda também é denominada velocidade de fase da onda.
Levando-se em conta a existência da corrente de deslocamento veremos a seguir que, utilizando-se de manipulações não muito complexas, as equações de Maxwell no espaço podem ser escritas sob a forma da equação de ondas. Este texto é disponibilizado nos termos da licença Creative Commons Atribuição-CompartilhaIgual 3. Não Adaptada (CC-BY-SA ). Para este fim, faremos uso dos teoremas de Gauss e Stokes discutidos na seção anterior.